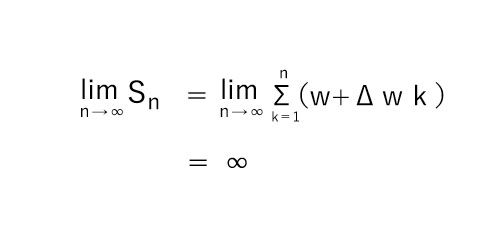作成日：2017/11/30 最終更新日：2021/01/08 かいたひと：ユーリー小松崎（蛸足大学文学研究科メタ研究心理学教室）
【作家日常】そういえば以前通っていた病院で「強風のため冬期はこちら側の入口を閉め切ります」という意味で写真のように「締切」という張り紙がべたべた貼られてた時期がありました。行くたびすごく怖かったのを冬がくると思い出します。https://t.co/LgbIYMkb0z pic.twitter.com/SSVyt3rLwj
— 松崎有理（作家）公式 (@yurimatsuzaki_n) 2017年12月7日
はじめに—締切と仕事量
パーキンソンの法則とは
「仕事は締切時間いっぱいまで膨張する」。これが一般にいわれるパーキンソンの法則である（1）。
ところがオリジナルである C. N. Parkinson の書いた論文（2）には上の一行は「法則」として紹介されていない。たんに論文冒頭で「常識的に観察されるもの」（大意）とかんたんに触れられているのみである。彼がじっさいに「パーキンソンの法則」として論文および著作（3-5）に書いているものは以下のとおりである：
- 第一法則 役人の数は仕事の量の多寡にかかわらず増大する
- 第二法則 金（かね）は入るだけ出ていく
原著論文（2）は第一法則について書かれている。ていねいに読めば、この論文は「仕事の量の多寡にかかわらず」という部分に力点を置いていることは容易にわかる。つまり「仕事の量が増加していく」ことは重視されていないのである。ところがなぜかこのオリジナルの第一法則は世間から無視にちかい扱いをうけている。その理由は他のところで述べた（6）のでここでは繰り返さない。
現状ほぼ無視されているオリジナル第一法則の存在を本稿では尊重したい。よって、一般に「パーキンソンの法則」と呼ばれているものに「第零法則」とあらためて名づけることにする（7）。
研究者の仕事と締切
さて、世の中のおおかたの仕事と同様、研究者の仕事にも締切が存在する。締切の性質によって仕事を分類すると以下のようになる：
- 締切をぜったいに延長することができない仕事
- 締切を延長可能な仕事
前者の代表がかけんひ申請書類であり、後者の代表が学術論文投稿である。かけんひの申請には通例11月という絶対的な締切があり、けっして動かすことはできない。遅れたらその年は申請不可能となる。いっぽう、学術論文の投稿には明確な締切が存在しない。研究室のボスや共著者にせっつかれたばあいをのぞき基本的に、論文が書きあがったときが締切である。
多くの研究者が実感していることであるが、前者の仕事にくらべ、後者の仕事では締切が延びれば延びるほどやるべきことが増殖していく印象がある（8）。具体的には、論文執筆のさい「まだなおしたい箇所があるから投稿は来月に延期しよう」ときめたとたん、あらたに引用したい文献が大量に発生する。これらをとりいれて「議論」や「はじめに」部分を書き直すのもたいへんな苦労である。議論部分がどうしてもしあがらないのでまた投稿を翌月に延期すると、そのころにはふたたび引用すべき新しい論文が発生している。以下、繰りかえし。悪くするとその論文はもう一生投稿することができない。
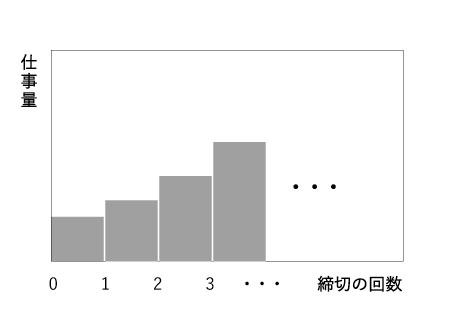
つまりパーキンソンの第零法則は、締切の延長のたびに強化されるのである。これを筆者は「研究者心理におけるパーキンソンの第零法則の拡張」と呼びたい。この現象を図解すると図１のようになる。
図１. 締切を引き延ばしているとき研究者の頭のなかに浮かぶグラフ。このままではいけないことは理解している。しているのだが。
しかし、以上はあくまで研究者たちの抱く印象にすぎない。これがまったくもって正しいことを厳密に証明することが本論文のねらいである。
方法—数学的帰納法とは
数学的帰納法とは、紀元前の哲学者集団・百歩七嘘派（9）により確立されたといわれるシンプルかつ強力な証明方法である。その基本方針は、ある命題P(n)がすべての自然数ｎについて成り立つことを証明したいとき：
i) P(1)が正しい
ii) ある自然数ｋについて、P(k)が正しいならばP(k+1)も正しい
以上ふたつを証明する。そうすると、ドミノだおしのようにn=1から順々にすべてのnについて命題Ｐが正しいといえることになる。
たとえば実例として、命題「すべてのひとはハゲである」を証明してみよう。
i) 髪の毛の本数n=1であるときそのひとがハゲであるのは自明。
ii) 髪の毛がｋ本のひとがハゲであるなら、そのひとに１本髪をたしたところで見た目は変わらないのでやはりハゲ。
よって、ｎ本の髪の毛をもつひとはすべてがハゲとなる（10, 11）。
髪の毛の本数と同様、締切の回数とはつねに自然数であるので、「研究者心理におけるパーキンソンの第零法則の拡張」を証明するには数学的帰納法はうってつけの方法である。
結果—数学的帰納法による証明
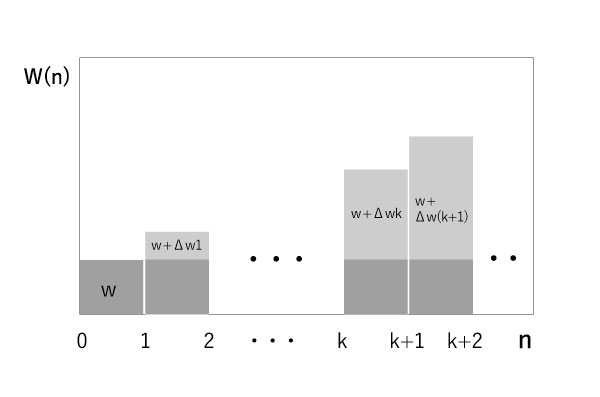
説明をわかりやすくするため、図１を改編して図２のようにする。
図２ 締切が延長されるごとに仕事量は増加することの数学的帰納法による証明。縦軸は仕事量ｗ、横軸は締切の回数ｎ。
命題「締切がn回延長されると、仕事の量はそのたび増加する」— (＊)
i) 締切1が締切2へ延長されると、仕事量wはw+Δw1へ増加する。
これはパーキンソンの第零法則により自明。
ii) kが任意の自然数であるとき、 締切kが締切(k+1)へ延長されると仕事量w+Δwkはw+Δw(k+1)に増加することが正しいとする。
締切(k+1)が締切(k+2)へ延長されると、
w+Δw(k+1)+[w+Δw(k+1)]+Δw1=w+Δw(k+2)
よってこのばあいも仕事量は増える。
ゆえに (＊)はすべての自然数nについて成立する。
よって、「研究者心理におけるパーキンソンの第零法則の拡張」は正しい。■
議論—締切が無限に延長されたらどうなるか
締切が延長されるたび新たに生まれる仕事量は、もとの仕事量に加算される。よってこれらは無限級数の和{Sn}であるとみなすことができる。ｎ→∞となるとき、{Sn}は無限大に発散する。
図３, 締切が無限に延長されるとき、仕事量も無限大となる。
仕事が無限（12）に増えるというおそろしい事実がわかったところで、これを回避することはかんたんである。締切を厳守し、いちどたりとも延長せねばよいのである。そうすれば仕事量の増加は最小限で済む。
結論
てきとうな時点であきらめることができるのも研究者の能力のうち。
引用文献
1, Bloch A. The Complete Murphy’s Law.
2, Parkinson’s Law. The Economist; Nov 19 1955
3, Parkinson CN. Parkinson’s Law.
4, Parkinson CN. The Law and The Profits.
5, Parkinson CN. The Law, or Still in Pursuit.
6, ユーリー小松崎 忘れ去られた「パーキンソンの第一法則」の謎：なぜ “役人数の増加” は法則の地位から滑り落ちたか メタ研究心理学雑誌 in press.
7, Asimov I. Robots and Empire.
8, Morgann JP. Personal communication.
9, 松崎有理 蛇足軒奇譚 角川書店; 2014
10, 松崎有理 かけだしどうし 代書屋ミクラ 光文社; 2015
11, ユーリー小松崎・松崎有理 比較生物学から導かれる無毛と長寿との関係——はげは長生き？ 架空論文投稿計画 光文社; 2017
12, 松崎有理 ５まで数える 筑摩書房; 2017
【作家日常】東京駅八重洲口もいまこんなことになってるんだけど、こういうばあいの表記って「締切り」ではなく「閉切り」が正しいのではないでしょうか。だいいち心臓に悪いし。https://t.co/LgbIYMkb0z pic.twitter.com/YYFw7lGQmR
— 松崎有理（作家）公式 (@yurimatsuzaki_n) 2018年2月12日
＊＊＊＊＊＊＊＊＊＊＊＊＊
この論文はフィクションです。実験データはすべて架空です。
この論文は拙著『架空論文投稿計画』収録のショートショート「研究者心理におけるパーキンソンの法則――メタ研究心理学者・ユーリー小松崎の事件簿」のスピンオフです。
こちらの架空論文もいかがですか：
理系男子チェックシャツ問題について最終的回答を与える
